QingZhi's Blog

Persistence is not easy

0%

动态规划_背包问题_完全背包理论

Posted on In , Views: Valine:

在掌握完全背包之前需要掌握01背包, 对于01背包问题的讨论,可以参考之前的文档; 这里在讲解完全背包, 主要以对比 01背包的方式进行;

问题定义

背包问题结构如下图;

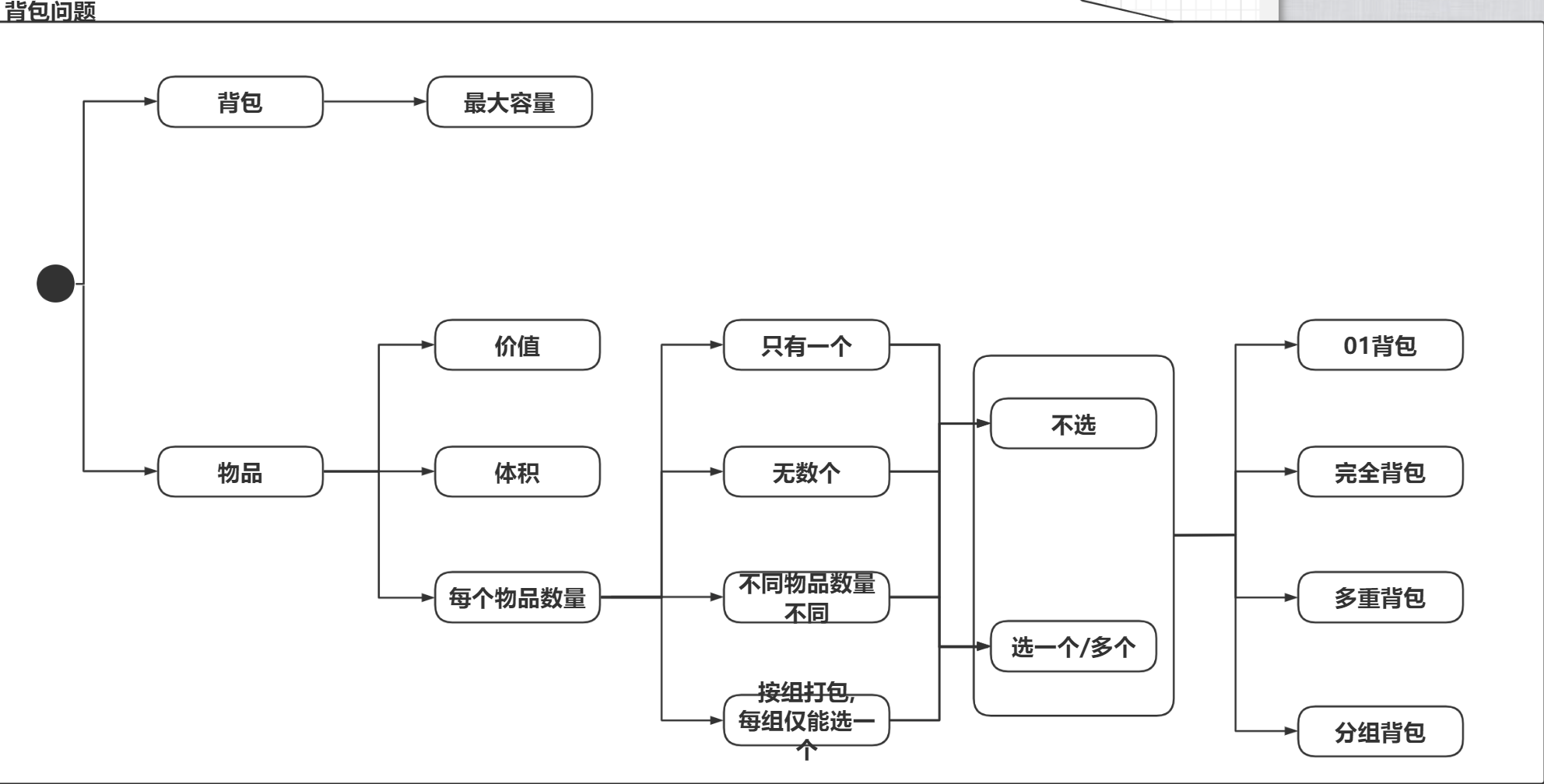
image-20220522163758857

可以发现完全背包相比较于01背包,唯一的不同点在于, 每件物品的数量时无限的;具体定义为:

问题定义: 有N件物品,和一个容量(衡量单位为重量)为W 的背包, 物品i 的重量为 weight[i], 价值为 value[i]. 每件物品数量无限制, 问这个背包可以装的最大价值是多少?

问题理解

这里以一道题目作为引子, 题目与 01背包类似, 只是物品数量无限制;

背包的容量为4, 物品的重量与价值如下表:

重量 价值
物品 0 1 15
物品 1 3 20
物品 2 4 30

要求返回背包的最大价值;

一维数组解法

由于已经有了 01背包 的铺垫, 这里不再讨论 二维数组解法;

动态规划三步走

这里的三步走跟 01背包 是一摸一样, 所以说完全背包与01背包的差距并没有体现在动态规划的定义上,而是体现在遍历顺序方面;

状态定义: dp[j] 定义为容量为 j 的背包所能够获得的最大价值;

状态转移方程: 在遍历过程中,也是对物品i的取舍问题:

注意这里对于物品的取舍是有陷阱的, 这里指的时当前对物品的取舍; 如果保证物品仅取舍一次,就是01背包问题, 如果保证物品尽可能的去取舍那就是完全背包问题;

  • 不放物品: dp[j] 不需要更新,本质与上述一致;
  • 放物品: dp[j] = dp[j-weight[i]]+value[i];

综上: dp[j] = max(dp[j], dp[j-weight[i]] + value[i])

边界

对于一维数组的边界,也就是dp[0] 那么直接为0 即可;

初始化与遍历顺序

数组初始化

状态定义为容量为 j 的背包所能够获得的最大价值, 那么在初始时赋值为0即可;

遍历顺序

在01背包的对应讨论部分, 我们已经知道对于背包的遍历, 如果正序遍历, 那么是完全背包, 如果是逆序遍历那么是01背包; 我们可以通过实践填充表格,印证这个结论;

在01背包中遍历顺序是固定的: 先遍历物品, 再遍历背包容量; (背包容量逆序遍历);而对于完全背包中的遍历顺序是任选的: 既可以先物品后容量, 也可以先容量后物品;

  • 先物品后容量的遍历:

    1
    2
    3
    4
    5
    for i := 0 ;i < len(weight) ; i++ {
        for j:= weight[i] ; j <= bagWeight ; j++ {
            dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
        }
    }

  • 先容量后物品的遍历:

    1
    2
    3
    4
    5
    6
    7
    for j:= 0 ; j <= bagWeight ; j++ {
        for i := 0; i<len(weight); i++ {
            if j >= weight[i] {
                dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
            }
        }
    }

    为什么完全背包 就没有这样的限制呢? 这是由于完全背包在遍历到当前点时, 需要保证左上方数据已经完全决定了即可; 相比较于 01背包 的逆序遍历背包容量, 完全背包 采用顺序遍历, 不管是哪一种优先遍历,均可以保证左上侧已经最终确定;

算法实例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
// test_CompletePack1 先遍历物品, 在遍历背包
func test_CompletePack1(weight, value []int, bagWeight int) int {
	// 定义dp数组 和初始化
	dp := make([]int, bagWeight+1)
	// 遍历顺序
	for i := 0; i < len(weight); i++ {
		// 正序会多次添加 value[i]
		for j := weight[i]; j <= bagWeight; j++ {
			// 推导公式
			dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
			// debug
			//fmt.Println(dp)
		}
	}
	return dp[bagWeight]
}

// test_CompletePack2 先遍历背包, 在遍历物品
func test_CompletePack2(weight, value []int, bagWeight int) int {
	// 定义dp数组 和初始化
	dp := make([]int, bagWeight+1)
	// 遍历顺序
	// j从0 开始
	for j := 0; j <= bagWeight; j++ {
		for i := 0; i < len(weight); i++ {
			if j >= weight[i] {
				// 推导公式
				dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
			}
			// debug
			//fmt.Println(dp)
		}
	}
	return dp[bagWeight]
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

func main() {
	weight := []int{1, 3, 4}
	price := []int{15, 20, 30}
	fmt.Println(test_CompletePack1(weight, price, 4))
	fmt.Println(test_CompletePack2(weight, price, 4))
}