QingZhi's Blog

Persistence is not easy

0%

最小生成树_Minimum-Spanning-Tree

Posted on In , Views: Valine:

最小生成树是图的应用之一，是无向有权图的最短路径算法。

图的应用有哪些？

最小生成树，最短路径，关键路径，拓扑排序，关键路径等。每种应用适用的场景不同，但是却很容易混淆，原因之一就是实践的太少。

最小生成树是什么？

生成树是图的极小连通子图，特点有二：

  1. 包括所有图中顶点，n个顶点；
  2. 包括尽可能少的边，n-1条边。

意味着增加一条边就会产生回路，减少一条边则非连通。

那么最小生成树就是所有生成树中，权值和最小的生成树，最小生成树的性质有三：

  1. 最小生成树不唯一；
  2. 最小生成树边的权值和是唯一的；
  3. 边的数量等于定点数量-1.

最小生成树的算法：Prim与Kruskal

Prim与Kruskal算法均是基于贪心的策略，两算法中均利用最小树中的性质：

  • 假设存在带权连通无向图， $ G = （V,E） $, $U$ 标识最小生成树中的节点集，$(u,v)$ 标识一条具有最小权值的边，其中$ u\in U , v\in (V-U) $ ,那么必然存在一颗包含有边$ (u,v) $ 的最小生成树。

    上面的性质乍看一下很是不好理解，但可以直接理解为一句话：当前权值最小的边一定会被选进最小生成树中。

大多数的算法均采用，加入边的方式进行设计，Prim与Kruskal也不例外。

Prim算法

算法思想：从点的角度找边

假设：存在一个无向有权连通图$ G=(V,E) $ , $V_{t}$ 代表最小生成树中的节点，$V_{out} = V - V_t$ 代表未被选入最小生成树的节点，$ E_{t} $ 代表生成树边的集合。

初始$ V_t = {u_0} , E_t ={} $,重复下个步骤：

  • 在所有$u\in V_t , v \in V_{out}$ 寻找最小的权值边$ e_{(u,v)}$ ,将此边加入到$E_{t}$中，节点$v$加入到$V_t$中。

直到$V_t = V$为止。

时间复杂度：$O(|V|^2)$，不依赖于边$E$ , 适合于边稠密的情况。

算法执行步骤如下图所示：

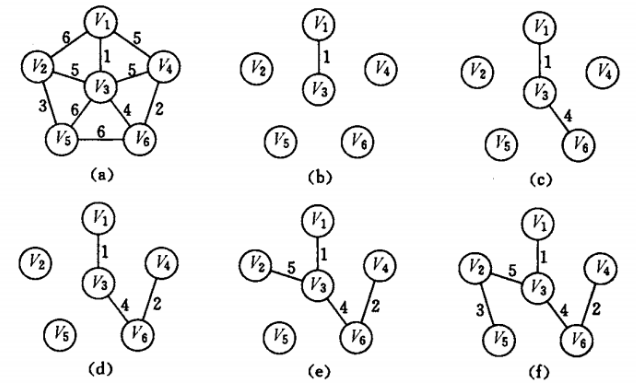
Prim算法示意图

代码步骤

参考地址：牛客网友回答

通过维护两个数组：

  • lowCost数组标识：$V_{t}$ 到所有节点的最小花销，如果该节点已经在$V_{t}$ 中，那么置为float(“inf”)；
  • VStatus数组标识：各节点的访问情况，初始化为0，若已访问则置为-1；
  1. 随机选择起点，加入到$V_t$中，更新lowCost与VStatus数组;
  2. 遍历lowCost数组，选择最小边（索引为j），将此边加入$E_{t}$,将此节点加入$V_{t}$,更新$lowCost[j]与VStatus[j]$
  3. 此时$V_t$ 已经发生了变化，需要更新所有的lowCost数组值；
  4. 重复第2步，直到所有的节点均已加入树中。

如图所示：

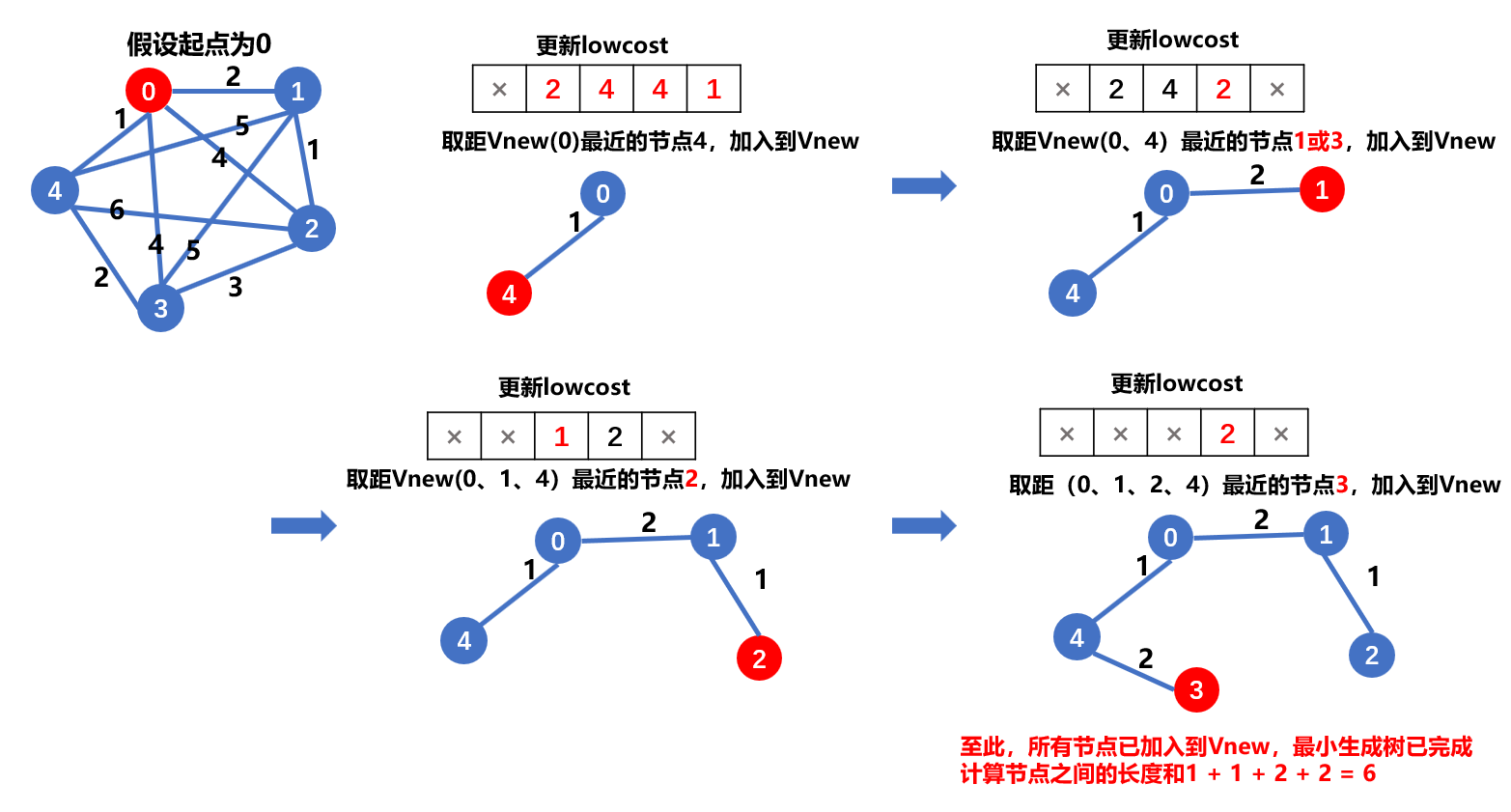
算法代码

以Leetcode1584题为例：

You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].

The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.

Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# Prim算法的常规实现形式，未使用堆。
class Solution:
    def minCostConnectPoints(self, points: List[List[int]]) -> int:
        def distance(pointA , pointB):
            return abs(pointA[0] - pointB[0]) + abs(pointA[1] - pointB[1])
        length = len(points)
        lowCost = [0 for _ in range(length)]
        vStatus = [0 for _ in range(length)]
        # 构造邻接矩阵方便之后的调用，非必须
        costMatrix = [[0 for i in range(length)] for _ in range(length)]
        for i in range(0 , length):
            for j in range(i+1 , length):
                dist = distance(points[i] , points[j])
                costMatrix[i][j] = costMatrix[j][i] = dist
        # 将第一个点加入V_t,并更新相关数组lowCost,vStatus
        vStatus[0] = -1
        lowCost[0] = float("inf")
        for j in range(1,length):
            lowCost[j] = costMatrix[0][j]
        output = 0
        # 寻找n-1次边
        for i in range(length-1):
            # 找到最小的边与索引
            minCost = min(lowCost)
            minIndex = lowCost.index(minCost)
            output += minCost
            # 更新lowCost[j] , vStatus[j]
            lowCost[minIndex] = float("inf")
            vStatus[minIndex] = -1
            # 更新所有的lowCost
            for i in range(length):
                if vStatus[i] != -1 and costMatrix[minIndex][i] < lowCost[i]:
                    lowCost[i] = costMatrix[minIndex][i]
        return output
  • 时间复杂度：$O(n^2)$,每一次在更新lowCost的复杂度均为$O(n)$.
  • 空间复杂度：$O(n^2)$.

Kruskal算法

算法思想:从边的角度触发

假设：存在一个无向有权连通图$ G=(V,E) $ , $V_{t}$ 代表最小生成树中的节点，$V_{out} = V - V_t$ 代表未被选入最小生成树的节点，$ E_{t} $ 代表生成树边的集合。

初始化：$V_t = V , V_{out} = \empty , E_t = {}$,每一个顶点是一棵树，此时的最小生成树是含有N棵树的森林。重复下面的步骤：

  • 按照图$ G$ 中权值递增的顺序从边$ E-E_t $ 选择边$e$ , 如果边并没有构成回路则添加进$E_t$ 中，否则舍弃此边。

直到$E_t$ 中包含有n-1条边。

  • 时间复杂度：$ |E|log|E| $,适合变稀疏的情况。

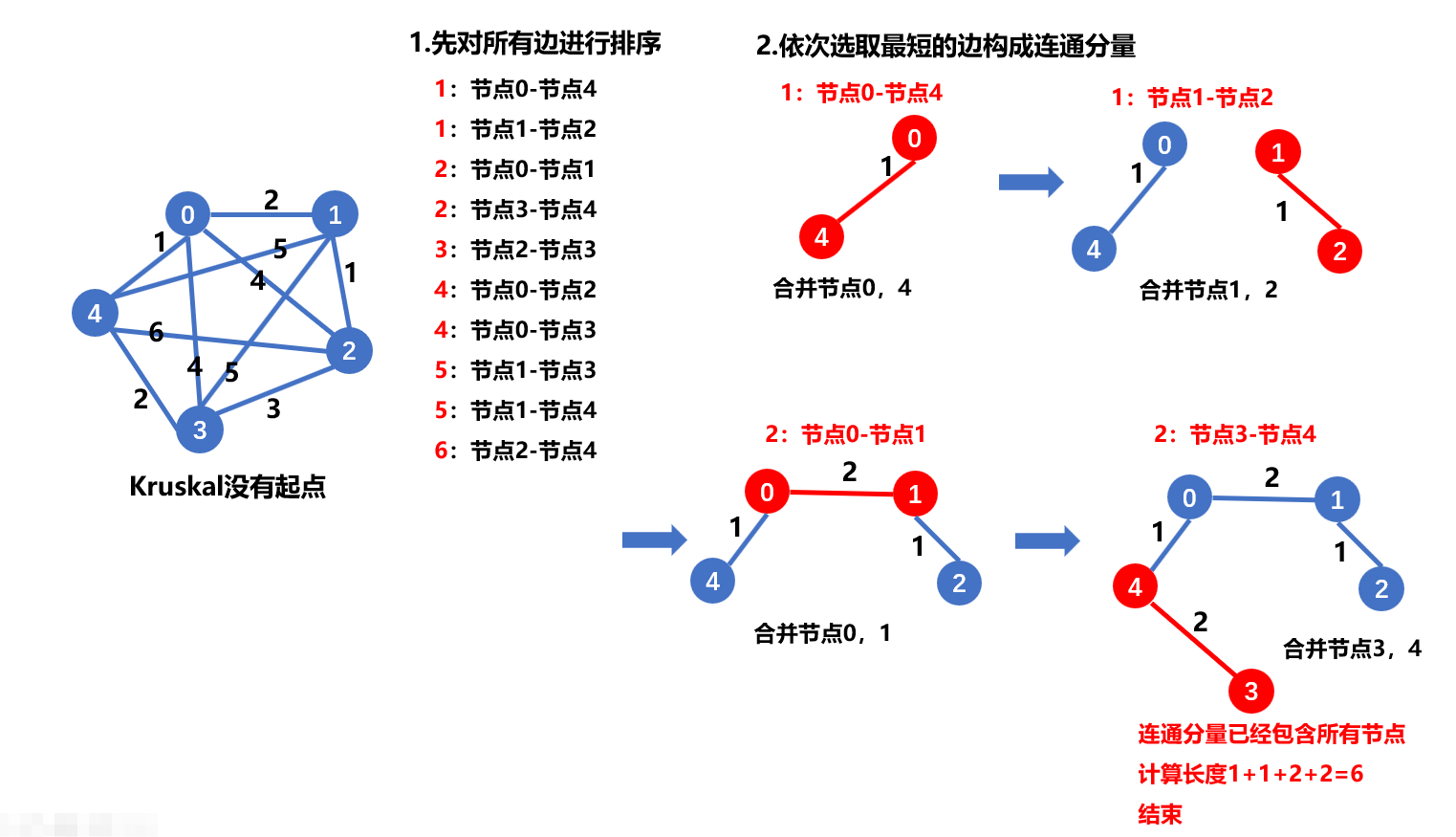
算法执行步骤如下图所示：

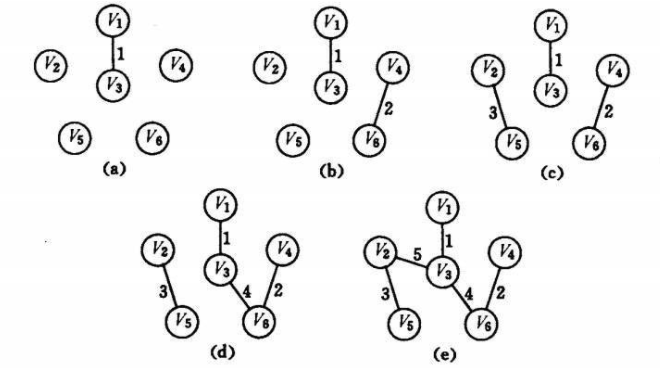
image-20210120133332552

代码步骤

利用并查集，很容易解决此类问题。并查集的定义与模板代码，可以看我的解释。

  1. 构建一个带有并查集的类，并实现相关功能；
  2. 计算所有的边长，并记录顶点信息，存储在数组$E$ 中，按照边长排序；
  3. 初始化并查集（将所有的顶点加入到并查集中）；
  4. 遍历$E$,假设每一个边由$e = [len , i , j]$ 组成：
    • 如果顶点$i，j$ 属于同一个集合，那么舍弃；
    • 否则进行集合合并操作，并累积output
  5. 返回output

算法代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# 同样以1584题为例
class Solution:
    def __init__(self):
        self.father = {}
    def add(self , x):
        if x not in self.father:
            self.father[x] = None
    def find(self , x):
        root = x
        while self.father[root]:
            root = self.father[root]
        while x != root:
            originalFather = self.father[x]
            self.father[x] = root
            x = originalFather
        return root
    def isConnect(self,x,y):
        return self.find(x)== self.find(y)
    def merge(self , x ,y):
        rootX = self.find(x)
        rootY = self.find(y)
        if rootX != rootY:
            self.father[rootX] = rootY
    def minCostConnectPoints(self, points: List[List[int]]) -> int:
        def distance(pointA , pointB):
            return abs(pointA[0] - pointB[0]) + abs(pointA[1] - pointB[1])
        length = len(points)
        # 边排序
        E = []
        for i in range(0 , length):
            for j in range(i+1 , length):
                dist = distance(points[i] , points[j])
                E.append([dist,i,j])
        E.sort(key = lambda k : k[0])
        # 初始化并查集
        for i in range(length):
            self.add(i)
        
        output = 0
        # 从小到大寻找边，如果构成回路则跳过，否则加入
        for e in E:
            if self.isConnect(e[1] , e[2]):
                pass
            else:
                output += e[0]
                self.merge(e[1],e[2])
            
        return output

  • 时间复杂度：$O(mlog(m) + m\alpha(m))$,m为索引对的数量
  • 空间复杂度：$O(n^2)$