QingZhi's Blog

Persistence is not easy

0%

并查集

Posted on In , Views: Valine:

最近在刷Leetcode（NO.399）过程中看到了并查集的概念，发现自己并不是很清楚其概念，故这里将相关概念总结如下：

知乎专栏、相关博客、牛客网友解释

并查集的概念

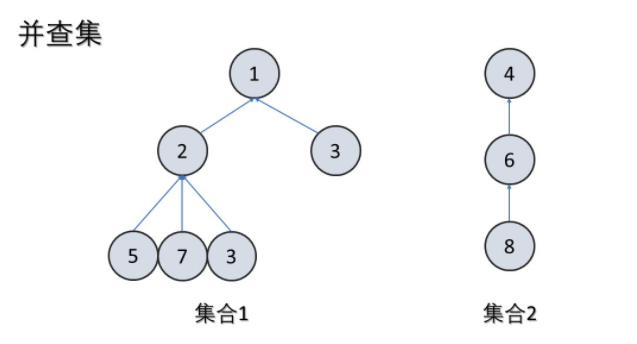
并查集首先是一种数据结构，在这种数据结构中其管理了一系列的不相交的集合，并且只存在合并与查询两种操作。有人将并查集如此解读：

  • 并(UNION):合并
  • 查(Find): 查找
  • 集(Set):一个以字典为基础的数据结构；

并查集跟树有些类似，只不过跟树是相反的。在树这个数据结构里面，每个节点会记录它的子节点。在并查集里，每个节点会记录它的父节点。

两种核心操作

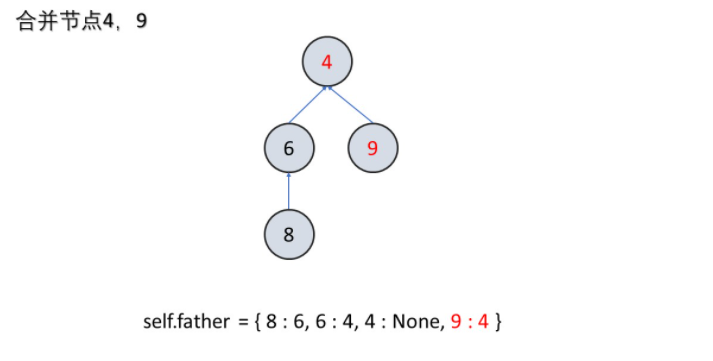
  • 合并：把两个不相交的集合合并为同一个集合
  • 查询：查询当前元素所属集合。

并查集核心思想

用集合中某元素来代表此集合，通常此元素为根节点。要想找到此集合的代表元素，就需要不断的寻找父节点，直到父节点为本身时，即为代表元素。

并查集中的概念梳理

来源于牛客网友解释

  • 并查集的初始化：利用字典记录父节点信息
1
2
3
4
5
6
class UnionFind:
    def __init__(self):
        """
        记录每个节点的父节点
        """
        self.father = {}

  • 并查集的连通性：在同一棵树里(祖先节点相同)，则说明两节点连通，如下图所示：

    image-20210120161137309

1
2
3
4
5
6
def is_connected(self,x,y):
    """
    判断两节点是否相连
    """
    return self.find(x) == self.find(y)
  • 添加节点：在字典实现中，需要置父节点为空即可。

image-20210120161401471

1
2
3
4
5
6
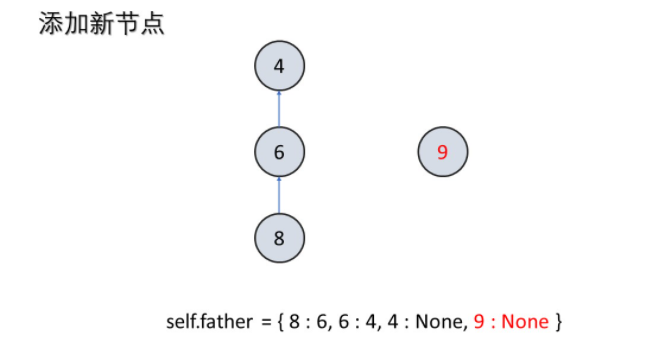
def add(self,x):
    """
    添加新节点
    """
    if x not in self.father:
        self.father[x] = None

  • 合并节点：合并节点就是将其祖先节点一致，可以任意加入对方的队伍。

    image-20210120161558452

1
2
3
4
5
6
7
8
9
def merge(self,x,y,val):
    """
    合并两个节点
    """
    root_x,root_y = self.find(x),self.find(y)
    
    if root_x != root_y:
        self.father[root_x] = root_y
  • 查找祖先：父节点不为空：不停的迭代或者递归均可以
1
2
3
4
5
6
7
8
9
10
11
  
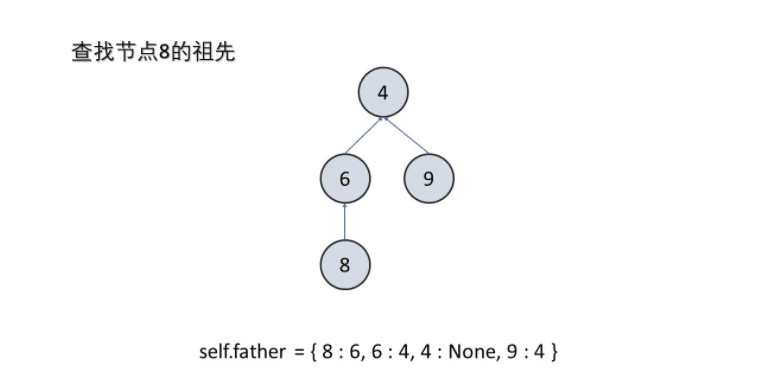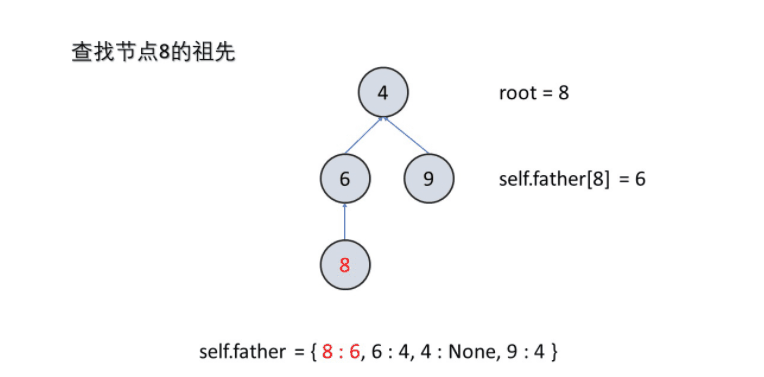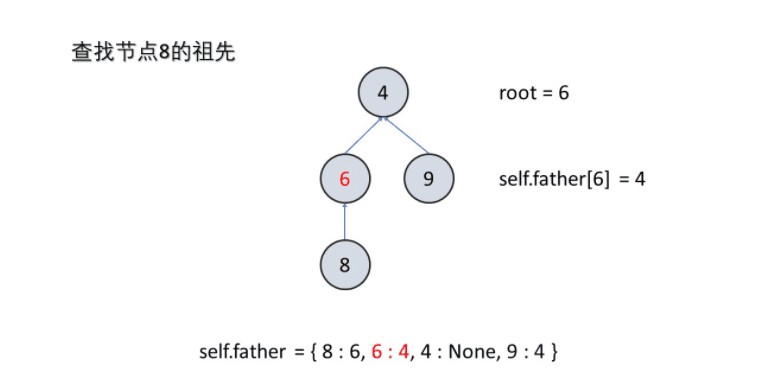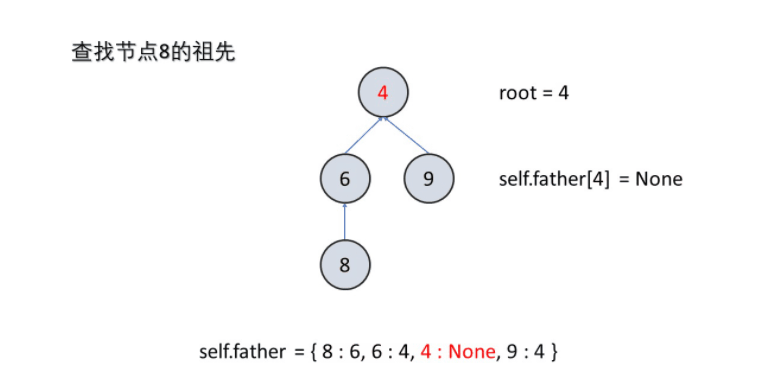
def find(self,x):
    """
    查找根节点
    """
    root = x
  
    while self.father[root] != None:
        root = self.father[root]
  
    return root

Union_Find

  • 路径压缩：查询时启动的路径优化算法，就是将路径上所有的节点直接连接到祖先节点

    Union_PassZip

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
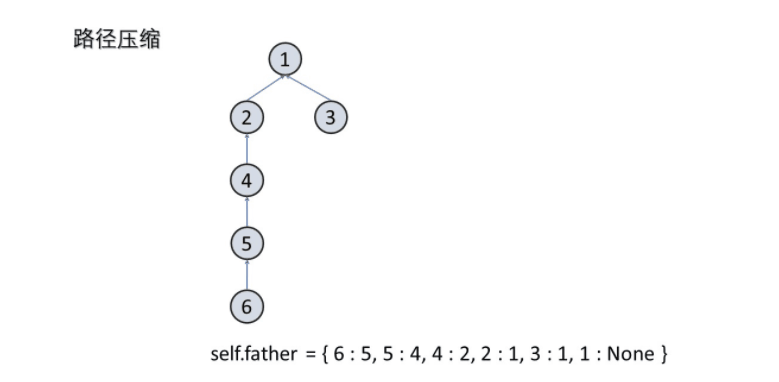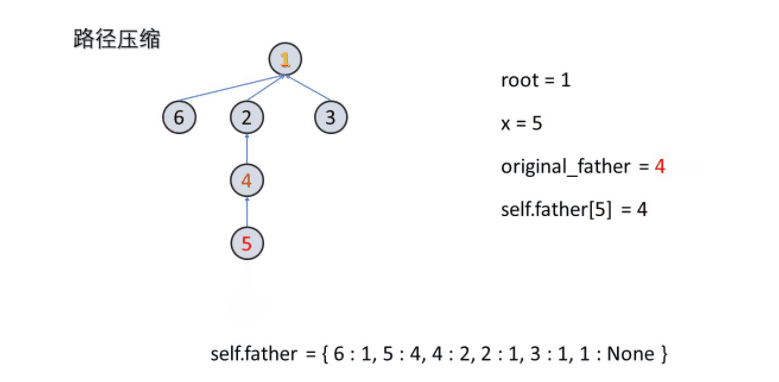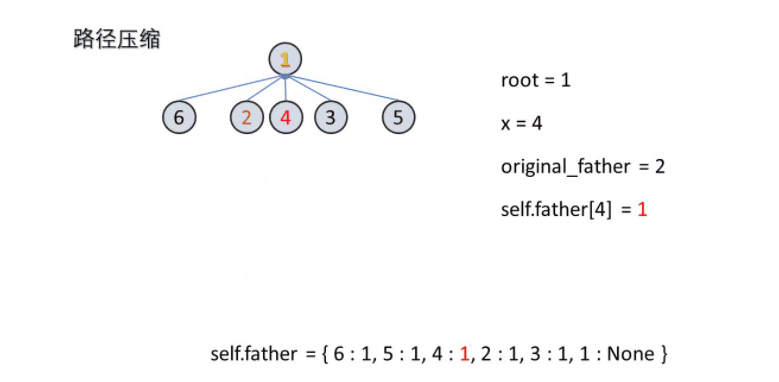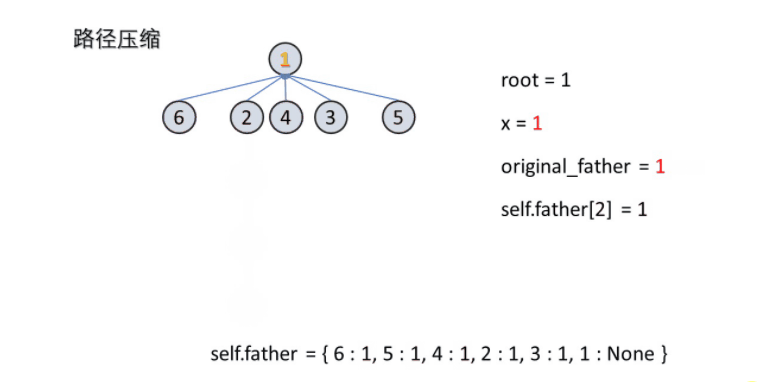
def find(self,x):
    """
    查找根节点
    路径压缩
    """
    root = x

    while self.father[root] != None:
        root = self.father[root]

    # 路径压缩
    while x != root:
        original_father = self.father[x]
        self.father[x] = root
        x = original_father
     
    return root

并查集的实现：

数组实现：

在知乎专栏介绍中，已经利用数组实现了并查集，不推荐使用。

  • 找到祖先节点的标志是：本身记为父节点。

  • 采用了递归的方式寻找祖先节点

    这里不再赘述。并且我个人认为数组的形式天然不适合作为并查集的实现方式，而字典这种键值对的方式更加适合实现并查集。

不建议适用数组实现

字典实现模板

这里提供字典的实现方式，并且祖先节点的标志为：自身的父节点为None时为祖先节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class UnionFind:
    def __init__(self):
        """
        记录每个节点的父节点
        """
        self.father = {}
    def find(self,x):
        """
        查找根节点
        路径压缩
        """
        root = x

        while self.father[root] != None:
            root = self.father[root]

        # 路径压缩
        while x != root:
            original_father = self.father[x]
            self.father[x] = root
            x = original_father
         
        return root
    
    def merge(self,x,y,val):
        """
        合并两个节点
        """
        root_x,root_y = self.find(x),self.find(y)
        
        if root_x != root_y:
            self.father[root_x] = root_y

    def is_connected(self,x,y):
        """
        判断两节点是否相连
        """
        return self.find(x) == self.find(y)
    
    def add(self,x):
        """
        添加新节点
        """
        if x not in self.father:
            self.father[x] = None