堆排序简介与用处

堆排序实在数据结构中常见的排序算法，但许久未看已经忘得差不多啦。这里简单的将相关概念记录如下：

[参考博客]（https://www.cnblogs.com/lanhaicode/p/10546257.html）

什么是堆

堆是利用完全二叉树的结构进行维护的一位数组，我们可以将其看作是一维数组也可以看作是完全二叉树，物理上是线性结构，理论上是非线性结构。

大顶堆：每个节点值大于或等于左右子节点的值
小顶堆：每个节点值小于或等于左右子节点的值
这也是堆最重要的特性

举个例子

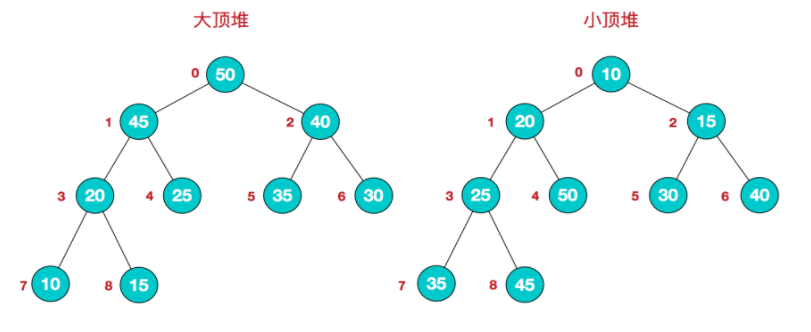
我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子.

公式定义：

大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]

小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

堆排序

堆排序是堆最常见的应用方式，堆排序的过程由三个步骤迭代完成。

堆的构建

初始堆的构建，是堆所有的非叶子节点进行调整，时间复杂度为$ O(n) $，自下而上
出堆
堆调整

堆调整只需要更改部分节点变化的节点即可，时间复杂度为$ O(log(n)) $ ,是自上而下的

升序：使用大顶堆

每个结点的值都大于或等于其左右孩子结点的值，我们把大顶堆构建完毕后根节点的值一定是最大的，然后把根节点的和最后一个元素（也可以说最后一个节点）交换位置，那么末尾元素此时就是最大元素了（理解这点很重要）
1. 先n个元素的无序序列，构建成大顶堆
2. 将根节点与最后一个元素交换位置，（将最大元素”沉”到数组末端）
3. 交换过后可能不再满足大顶堆的条件，所以需要将剩下的n-1个元素重新构建成大顶堆
4. 重复第二步、第三步直到整个数组排序完成
降序 :使用小顶堆

代码示例

代码中展示了通过一个大顶堆,构建升序的过程,具体的展示可以见排序算法总结.md,gif图生动的展示了过程.

# 构建大顶堆的节点交换函数,作为辅助函数
def oneStep(nums , n , i):
    index = i
    left = i*2 + 1
    right = i*2 + 2
    if left < n and nums[left] > nums[index]:
        index = left
    if right < n and nums[right] > nums[index]:
        index = right
    if index != i:
        nums[i] , nums[index] = nums[index] , nums[i]
        oneStep(nums , n , index)
# 构建堆函数,自下而上
def buildHeap(nums):
    for i in range(len(nums)//2-1 , -1 , -1):
        oneStep(nums , len(nums) , i)
    
nums = [7,2,3,5,6,1,9,10,0]
buildHeap(nums)
# 不断的出堆,堆调整(自上而下)
for i in range(len(nums)):
    nums[0] , nums[len(nums)-1-i] = nums[len(nums)-1-i] ,nums[0]
    oneStep(nums , len(nums)-1-i , 0)
print(nums)

QingZhi's Blog

堆排序简介与用处

什么是堆

举个例子

相关易混淆概念

堆排序

代码示例