二维前缀和

Leetcode讲解

在二维数组中涉及到大量计算某区域的算法题目，为了降低时间复杂度，对数组区域进行记忆是必不可少的，这也就提出了二维数组的前缀和（P）概念。

在得到P的同时，我们可以在 $O（1）$ 的时间复杂度内，得到任意矩形区域的和。

推导过程

假设二维数组的 $ A $ 的大小为 $ m * n $ ,其数组下标的范围为$ [1 \dots m] , [1\dots n]$.

数组下标范围与真实程序中的范围存在偏差，这样写主要为了与后面P数组对应，容易理解。

数组 $ P $ 是 $ A $ 的前缀和数组，$ P $ 中每一个元素 $ P[i][j] $ 均符合以下定义：

• 如果 $ i , j $ 均大于 0 ，那么 $ P[i][j] $ 表示数组 $A $ 中以 $ [1,1] $为左上角 ， $ [i , j] $ 为右下角的矩形区域的元素和。
• 否则，$ P[i][j] $ 等于 0 .

在这里我们就可以发现，$ P $ 数组其实比 $ A $ 数组多了一行一列，并且是在第一行前、第一列前添加了 0 行/列， 这么做是为了计算的统一性。

任意矩形区域的计算

在得到完整的$ P $ 数组之后，我们可以在常数时间内得到你想要的任意的矩形区域的元素和。我们假设其矩形区域的右上角为 $ (x_1 , y_1) $ ,左下角为 $(x_2 , y_2) $ . 有
$$
sum = A[x_1\dots x_2][y_1 \dots y_2] = P[x_2][y_2] - P[x_1-1][y_2] - P[x_2][y_1-1] + P[x_1 - 1][y_1 -1]
$$

上式中我们看到其大量的采用 了 - 1的形式，在面对边界时如果P数组不扩充，就会出现数组越界问题。

证明上式：

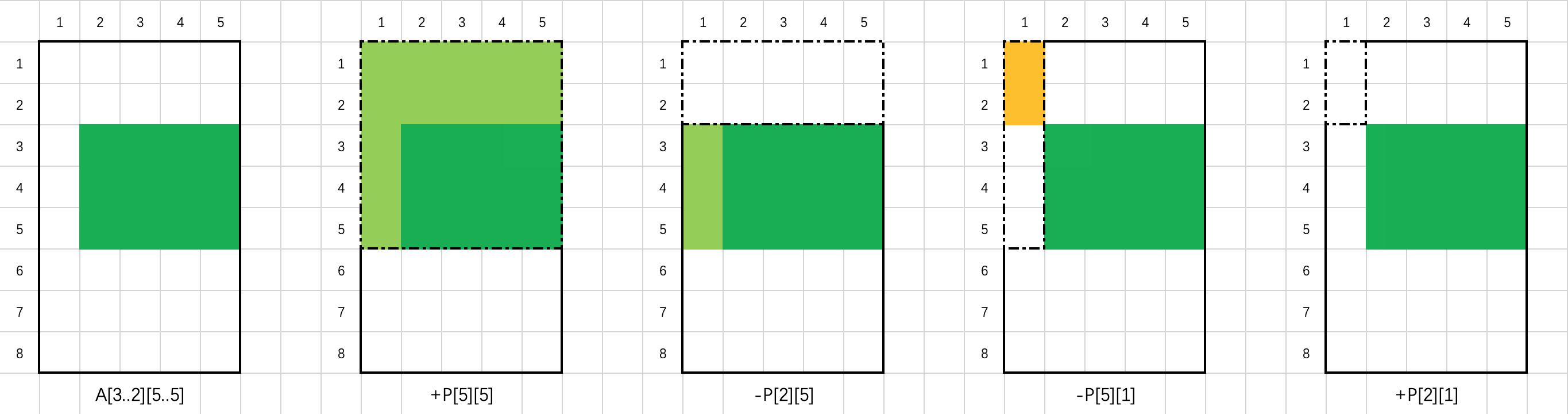
以下图为例，当 A 的大小为 8 * 5，需要求和的矩形区域（深绿色部分）的左上角为 (3, 2)，右下角为 (5, 5) 时，该矩形区域的元素之和为 P[5][5] - P[2][5] - P[5][1] + P[2][1]。

数组P的获取

上面讲了数组$ P $ 的应用，那么数组 $P $ 到底是怎么得到的呢？

还是利用上面的式子有：

我们按照行优先的顺序依次计算数组 P 中的每个元素，即当我们在计算 P[i][j] 时，数组 P 的前 i - 1 行，以及第 i 行的前 j - 1 个元素都已经计算完成。此时我们可以考虑 (i, j) 这个 1 * 1 的矩形区域，根据上面的等式，有：
A[i][j] = P[i][j] - P[i - 1][j] - P[i][j - 1] + P[i - 1][j - 1]
由于等式中的 A[i][j]，P[i - 1][j]，P[i][j - 1] 和 P[i - 1][j - 1] 均已知，我们可以通过：
P[i][j] = P[i - 1][j] + P[i][j - 1] - P[i - 1][j - 1] + A[i][j]

代码实现

注意真实数组下标问题

def getPresum(nums):
    m = len(nums)
    n = len(nums[0])
    P = [[0 for _ in range(n+1)] for _ in range(n+1) ]
    for i in range(1 , m+1):
        for j in range( 1, n+1):
            P[i][j] = nums[i-1][j-1] + P[i-1][j] + P[i][j-1] - P[i-1][j-1]
    return P